5 Ejemplos de Propiedad del Inverso Aditivo: Aprende Fácilmente

La propiedad del inverso aditivo es uno de los conceptos fundamentales en matemáticas que nos permite comprender y operar con diferentes tipos de números. Comprender esta propiedad es esencial para el estudio de operaciones algebraicas y nos permite resolver problemas de manera más eficiente.

En este artículo, exploraremos la propiedad del inverso aditivo a través de 5 ejemplos prácticos. Desde números enteros hasta álgebra, analizaremos cómo se aplica esta propiedad en diferentes contextos y cómo podemos utilizarla para simplificar operaciones matemáticas.

Ya sea que estés estudiando para un examen, te estés preparando para una competencia matemática o simplemente quieras mejorar tus habilidades en matemáticas, este artículo te ayudará a comprender y dominar la propiedad del inverso aditivo.

¿Qué es la propiedad del inverso aditivo?

La propiedad del inverso aditivo establece que para cada número real, existe otro número real que, al sumarlo al número original, da como resultado cero. En otras palabras, el inverso aditivo de un número es aquel que, al sumarlo a dicho número, nos da como resultado cero.

Esta propiedad se puede expresar matemáticamente de la siguiente manera: para todo número real "a", existe otro número real "-a" tal que "a + (-a) = 0". El número "-a" es el inverso aditivo de "a".

Esta propiedad es esencial en matemáticas, ya que nos permite realizar operaciones como la resta y simplificar expresiones algebraicas. A continuación, exploraremos diferentes ejemplos para comprender mejor esta propiedad y su aplicación en diferentes contextos.

Ejemplo 1: Números enteros

En el contexto de los números enteros, la propiedad del inverso aditivo se aplica de la siguiente manera: para cada número entero "n", existe otro número entero "-n" tal que "n + (-n) = 0".

Por ejemplo, si tenemos el número entero 5, su inverso aditivo sería -5, ya que 5 + (-5) = 0. De manera similar, si tenemos el número entero -3, su inverso aditivo sería 3, ya que -3 + 3 = 0.

¿Cómo se define economía? Descubre el significado y conceptos clave

Esta propiedad es especialmente útil cuando realizamos operaciones de resta con números enteros. Por ejemplo, si queremos restar 7 a 10, podemos utilizar la propiedad del inverso aditivo para convertir la resta en una suma: 10 + (-7) = 3.

Ejemplo 2: Fracciones

En el caso de las fracciones, la propiedad del inverso aditivo también se aplica. Para cada fracción "a/b", existe otra fracción "-a/b" tal que "a/b + (-a/b) = 0".

Por ejemplo, si tenemos la fracción 3/4, su inverso aditivo sería -3/4, ya que 3/4 + (-3/4) = 0. De manera similar, si tenemos la fracción -2/5, su inverso aditivo sería 2/5, ya que -2/5 + 2/5 = 0. Esta propiedad nos permite simplificar operaciones de suma y resta con fracciones.

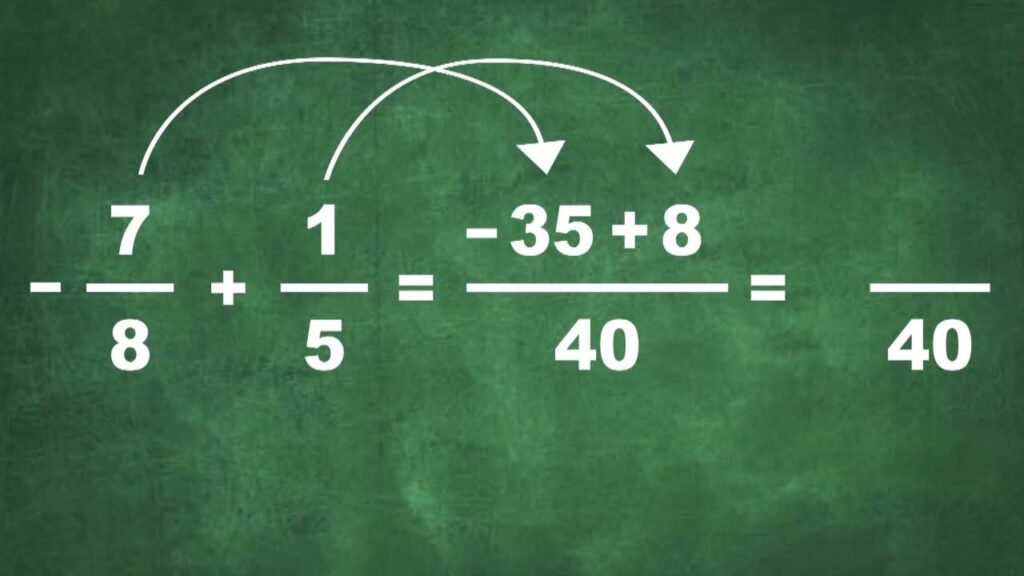
Por ejemplo, si queremos restar 1/2 a 3/4, podemos utilizar la propiedad del inverso aditivo: 3/4 + (-1/2) = 3/4 - 1/2 = 3/4 - 2/4 = 1/4.

Ejemplo 3: Números decimales

La propiedad del inverso aditivo también se aplica a los números decimales. Para cada número decimal "a", existe otro número decimal "-a" tal que "a + (-a) = 0".

Por ejemplo, si tenemos el número decimal 0.7, su inverso aditivo sería -0.7, ya que 0.7 + (-0.7) = 0. De manera similar, si tenemos el número decimal -1.5, su inverso aditivo sería 1.5, ya que -1.5 + 1.5 = 0. Esta propiedad nos permite simplificar operaciones de suma y resta con números decimales. Por ejemplo, si queremos restar 0.3 a 1.2, podemos utilizar la propiedad del inverso aditivo: 1.2 + (-0.3) = 1.2 - 0.3 = 0.9.

Ejemplo 4: Álgebra

La propiedad del inverso aditivo también se aplica en álgebra, donde trabajamos con variables y expresiones algebraicas. En este contexto, la propiedad del inverso aditivo nos permite simplificar operaciones y resolver ecuaciones. Por ejemplo, si tenemos la expresión algebraica "2x + 5", su inverso aditivo sería "-2x - 5", ya que (2x + 5) + (-2x - 5) = 0.

Al sumar estas dos expresiones, las variables "x" se cancelan y obtenemos como resultado cero. Podemos utilizar esta propiedad para resolver ecuaciones algebraicas. Por ejemplo, si tenemos la ecuación "3x + 7 = 10", podemos restar 7 a ambos lados de la ecuación utilizando la propiedad del inverso aditivo: (3x + 7) + (-7) = 10 + (-7) => 3x = 3 => x = 1.

Conclusión

La propiedad del inverso aditivo es fundamental en matemáticas y nos permite realizar operaciones de suma y resta de manera más eficiente. A través de los ejemplos presentados en este artículo, hemos visto cómo se aplica esta propiedad en diferentes contextos, desde números enteros hasta álgebra.

Es importante comprender y dominar esta propiedad, ya que nos permite simplificar operaciones matemáticas y resolver ecuaciones. Ya sea que estés estudiando para un examen, te estés preparando para una competencia matemática o simplemente quieras mejorar tus habilidades en matemáticas, la propiedad del inverso aditivo es un concepto esencial que debes dominar.

Así que no pierdas más tiempo y practica la propiedad del inverso aditivo con diferentes ejercicios y problemas matemáticos. Cuanto más practiques, más fácil será aplicar esta propiedad y resolver problemas de manera eficiente.

Preguntas frecuentes

1. ¿Qué sucede si no se cumple la propiedad del inverso aditivo?

Si no se cumple la propiedad del inverso aditivo, significa que no existe un número que, al sumarlo al número original, nos dé como resultado cero. En este caso, no podríamos realizar operaciones de resta o simplificar expresiones algebraicas utilizando esta propiedad.

2. ¿Es lo mismo el inverso aditivo que el inverso multiplicativo?

No, el inverso aditivo y el inverso multiplicativo son conceptos diferentes. El inverso aditivo se refiere a un número que, al sumarlo al número original, nos da como resultado cero. Por otro lado, el inverso multiplicativo se refiere a un número que, al multiplicarlo por el número original, nos da como resultado uno. Por ejemplo, el inverso aditivo de 5 es -5, mientras que el inverso multiplicativo de 5 es 1/5.

3. ¿Cuáles son las aplicaciones prácticas de la propiedad del inverso aditivo?

La propiedad del inverso aditivo tiene diversas aplicaciones prácticas en matemáticas y en la vida cotidiana. Algunas de las aplicaciones más comunes incluyen la resolución de problemas de suma y resta, la simplificación de expresiones algebraicas y la resolución de ecuaciones.

4. ¿Cómo puedo practicar la propiedad del inverso aditivo?

Para practicar la propiedad del inverso aditivo, puedes realizar ejercicios y problemas matemáticos que impliquen la suma y resta de diferentes tipos de números. Puedes utilizar ejercicios en papel, recursos en línea o incluso crear tus propios problemas. Recuerda que cuanto más practiques, más familiarizado estarás con esta propiedad y más fácil será aplicarla en diferentes contextos.